INTRODUCTION
IT begins as all begins - a random thought, perhaps a dream - some fragment of the man within. You take it and examine it and expand upon it. It grows and grows, and suddenly - there it is.
You are climbing a mountain of life - onward and upward, following the winding paths, dodging the pitfalls, skirting the boulders, charting yet uncharted regions - enjoying the beauty and adventure of the search. The height increases, the view broadens, the perspective clears - a few short steps, and you have reached the peak.
And then you must decide whether forever more this shall remain with you alone or whether it shall be communicated to others - and you decide that it shall be communicated.
You are there and you know you are there - but how? You stand at the peak of your mountain and look below upon a complete but undefinable thing. At the base there are so many approaches - so many different yet similar paths - all, in time, ending at your feet.
And so you take this dream - this living breathing piece of you - and chop it up, so to speak, into small finite bits that seem to "fit" together and in this form present it to the people with the hope that someday they may put them all together and see the dream themselves.
The responsibility then falls upon the reader to take these pieces of a living jigsaw puzzle and put them all together. However, even those most adept in this patient but mechanic art shall never find the view in this alone For, in the chopping and the sorting, some small bits are always lost. And so, upon the reader, falls a second, greater burden - to call upon that source which lights the way for him alone and find the missing parts.
Before you, in the following pages, is a kit which we have chosen to call Plan Theory. The bits and pieces are there, neatly packaged in bundles labeled Sections and Chapters, together with instructions for assembly and some oratory to hint of the view to come.
As you proceed through the text, opening each bundle and absorbing its contents, you should realize that each is but a fragment of the whole.
The view broadens, the perspective clears, the extremes fold to the
middle - and there it is.
| SECTION | CHAPTER | CONTENTS |
| ONE | MECHANICS | |
| ONE | GENERAL FUNCTIONS | |
| TWO | INORGANIC FUNCTIONS | |
| THREE | NATURAL ORGANIC FUNCTIONS | |
| TWO | S L PHILOSOPHY | |
| FOUR | INVERSE LAWS | |
| FIVE | CYCLE THEORY | |
| SIX | THEORETICAL SOCIAL SYSTEMS | |
| SEVEN | TRANSIENT SPACES | |
| THREE | G C PHILOSOPHY | |
| EIGHT | BASIC CONCEPTS | |
| NINE | SPECIAL THEORY OF ABSOLUTES | |
| TEN | GENERAL THEORY OF ABSOLUTES | |
| APPENDIX | FINAL EXAMINATION |
PREFACE
Ever since the dawn of man, individuals over the ages have probed the secrets of the universe. In the course of time, the great philosophers have come and gone, leaving a heritage of theories and predictions for those who followed them. The great masses of the Earth have been enslaved and freed, bought and sold and again sold in the gigantic complex of forces which constitute our environment. Each man in his time chooses one of the many winding paths and begins his journey, slowly climbing the mountain of life.
PLAN THEORYLet us now thrust our pick into the mountain of life and begin our climb. Let us follow the winding, twisting paths and forge our way towards the peak. The road is not an easy one. Along the way lie the massive traps and pitfalls of life. We shall endeavor to search out these and skirt about them. If we succeed, we shall be one of the privileged few who has had the opportunity to look down from the peak of the mountain upon the masses of the universe and see all things, for the first time, in their true perspective.
SECTION ONE
MECHANICS
PLAN THEORY
CHAPTER ONE
GENERAL FUNCTIONS
SET THEORY
DEFINITIONS OF STANDARD SEQUENCES
ALPHA SEQUENCE - Alphabetical Order
GAMMA SEQUENCE - Chronological Order
DELTA SEQUENCE- Continuity Order
SET THEORY
BASIC TERMS
To avoid the creation of a loop in the Delta sequence of our definitions, we shall treat the term 'set' as an undefined term in this text. Instead, we say that a SET is a collection of certain elementary components called MEMBERS . These members may be of two basic types, tangible and intangible. We refer to intangible members of a set as DATA and to tangible members, as MATTER. If some of the members of a set are matter, the set may be referred to as a STRUCTURE.
TYPES OF SETS
A set may contain many members, simply one member, or no members at all. If a set contains no members, it is called an EMPTY SET and is symbolized by "0". A non-empty set is said to be FINITE if all of its members can be completely described, listed, cataloged, etc. by ordinary methods; if this cannot be done it is said to be INFINITE. If a set contains all members, i.e., all data and mater in a specified area, it is referred to as a UNIVERSAL SET. In a technical sense, the "specified area" must be "our entire universe", but, in a more general sense, it may be any area.
SUBSETS
A set, A, is said to be a SUBSET of another set, B, if and only if set B contains every member of set A. The prefix "sub-" suggests that there would be at least one member of set B which was not contained in set A. If this is the case, set A is said to be a PROPER SUBSET of set B or, simply a subset of set B. It is possible, however, that every member of set A is a member of set B and every member of set B is a member of set A, i.e., they are identical. Technically, in this case, set A would still be considered a subset of set B but, to distinguish it from the more probable case, it is called an IMPROPER SUBSET.
COMPLEMENTS
The ABSOLUTE COMPLEMENT of a set, A, is that set, denoted by A', which contains every member of the technical universal set which is not contained in set A. The absolute complement, then, is the complement of a set with respect to the Universe. Although this type of complement has definite uses, we will be concerned mainly with the complement of a set with respect to another set, the relative complement. The RELATIVE COMPLEMENT of a set, A, with respect to another set, B, is that set, denoted by A'B, which contains those and only those members of set B which are not contained in set A.BASIC NOTATIONS
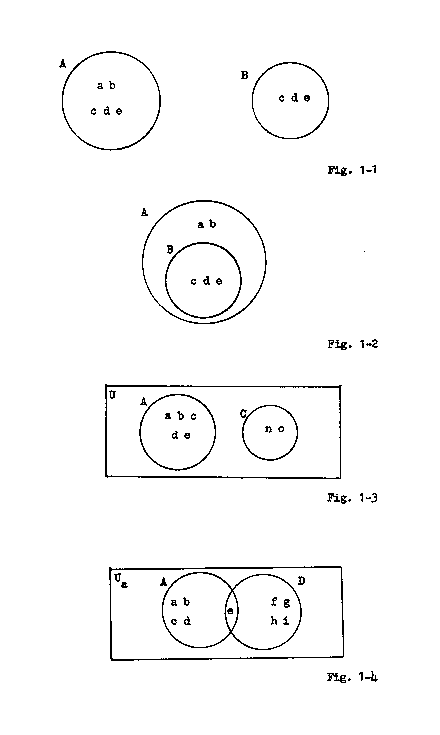
Certain elementary notations are used in set theory, some of which are illustrated by figures 1-1, 1-2, 1-3 and 1-4. References to specific sets in the following discussions refer to these figures.
Sets are usually identified by capital letters of the English alphabet. Average sets, such as set A, are diagrammed as circles and their members (if any) are specified (if desired) by placing their names or identifying symbols within the circle. Universal sets are diagrammed as rectangles and are identified by a symbol placed in the upper left hand corner. In the case of a technical universal set, such as the set in figure 1-3, the single letter "U" is used. In the case of a general universal set, such as that shown in figure 1-4, the symbol "U" is used with a subscript giving the sets' name or identifying symbol.
If it is desired to list the members of a set, they are placed in brackets, e.g., the members of set A would be listed as {a,b,c,d,e}. All members of a set need not be listed if the set has many members and they form some obvious sequence. For example, the set consisting of the letters of the English alphabet could be listed {a,b,c, ... ,x,y,z}, the "..." standing for the omitted letters.
Subsets
When sets having members in common are diagrammed, it is customary to show the sets "mapped over" one another to illustrate their configuration. For example, since set B is a subset of set A, the two sets could be diagrammed either as they are in figure 1-1 or as they are in figure 1-2 but, in figure 1-2 their relationship is more obvious.
Complements
Diagrams are particularly helpful in illustrating complements- especially relative complements. Examples of complements in the figures below are:
Absolute
A' is all data and matter in this Universe except the first five letters of the English alphabet.
Relative
B'A is {a,b}
A'B is {0}
A'C is {n,o}
A'D is {f,g,h,i}
D'A is {a,b,c,d}

BASIC OPERATIONS
If one is given a non-empty set, there are only two basic things that one can "do to it". One can either add members to it or delete members from it. We refer to the act of adding members to a set as PROGRAMMING and to the act of deleting members from a set as REPROGRAMMING. When one or both of these operations are performed upon a set and the exact operation(s) are unknown or are irrelevant, we say that the set is MODIFIED.
STATIC STATES
A set is referred to as STATIC if it is not undergoing programming or reprogramming. If the diagrams of two static sets, A and B, are mapped over one another, there are only three basic configurations that can occur. The two sets can have no members in common, some members in common, or all members in common.

SPECIAL OPERATIONS
Besides the two fundamental operations we discussed earlier, programming and reprogramming, there are two special types of modification that we will use throughout this text, union and integration.
Union
If a previously empty set is programmed with the members of two sets, A and B, then the previously empty set is said to be the UNION of the two sets, A and B, and is denoted by A U B. Union, then, is a kind of "set addition". In the process of forming set A U B, not necessarily all of the members of the two sets, A and B, were used. If they were all used, i.e., if both set A and set B are subsets of set A U B, then the two sets are said to have been MERGED. However, if set A and/or set B is not a subset of set A U B, i.e., some members were deleted in the process, the two sets are said to have been COLLATED.
Integration
Let us consider the two sets A and D shown in figure 1-4. If we program
set D with the members a, b, c, and d (from set A) and we also program
set A with the members f, g, h, and i (from set D), then the two sets will
become congruent.
Similarly, if we reprogram set A to delete the members a, b, c, and
d and we also reprogram set D to delete the members f, g, h, and i, the
two sets will also become congruent. Note that in both processes we have
been dealing with relative complements;
{a,b,c,d} is D'A and {f,g,h,i} is A'D. This
method of modifying two non congruent sets so that they become congruent
is called INTEGRATION.
As we have seen, one may integrate two sets by either programming or reprogramming. These two methods are formally presented in the following properties.
PR-1-1 Integration Through Programming
Given two non congruent sets, A and B:
If set A is programmed with A'B and set B is programmed with B'A, then the two sets, A and B, will become congruent.
PR-1-2 Integration Through Reprogramming
Given two non congruent sets, A and B:
If set A is reprogrammed to delete B'A and set B is reprogrammed to
delete A'B, then the two sets, A and B, will become congruent.
DYNAMIC STATES
A set is referred to as DYNAMIC if it is undergoing programming or reprogramming.
Congruence and Complementary State

Intersection
Like static sets, two dynamic sets may also intersect. However, in this case, there are two basic possibilities. Consider the case of the two sets, A and D, shown in figure 1-4. If we agree that both of these sets are dynamic, then members are continually being added to them and/or deleted from them. Let us suppose that set A is programmed with a member and set D is programmed with a member. If the members are congruent, the sets will tend to get "closer together"; if they are not congruent, the sets will tend to get "farther apart". Similarly, if each of the sets is reprogrammed to delete one member they will tend to get closer together if the members deleted were not contained in their intersection and farther apart if they were. In this case, if the latter were true, the two sets would become complementary.
When dealing with dynamic sets, then, it is convenient to split the state of intersection into two separate cases. Two non congruent dynamic sets are said to CONVERGE if they continually approach a congruent state and to DIVERGE if they continually approach a complementary state. If two dynamic sets, A and B, converge, the relationship is denoted by A< B; if they diverge, the relationship is denoted by A > B. Both notations are commutative.
Properties
The conditions under which two dynamic sets will remain congruent or complementary, or will converge or diverge under programming and under reprogramming are given in eight properties which treat all primary cases.
These properties follow, concluding our discussion of set theory.
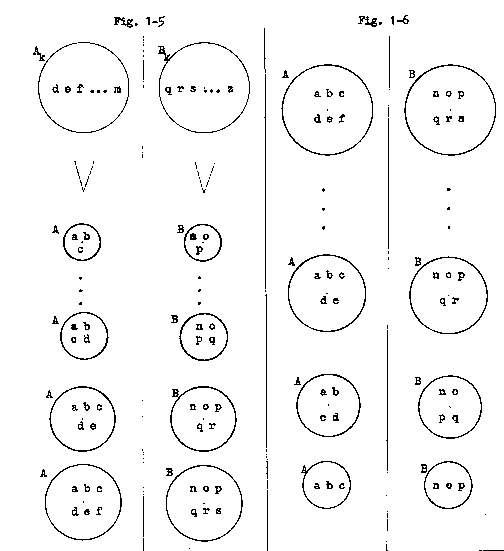
PR-1-3 Invariance From Complementary State Under Programming (Fig. 1-5)
Given four sets, A, Ak, B and Bk, such that no two of the sets intersect:
If, periodically, set A is programmed with a member of Ak and set B is programmed with a member of Bk, then the two sets, A and B, will remain complementary.
PR-1-4 Invariance From Complementary State Under Reprogramming (Fig. 1-6) Given two complementary sets, A and B.
If, periodically, set A is reprogrammed to delete one of its members and set B is reprogrammed to delete one of its members, then the two sets, A and B, will remain complementary.
PR-1-5 Invariance Prom Congruence Under Programming (Pig. 1-7)
Given four sets, A, Ac, B and Bc such that set A is congruent to set B and set Ac is congruent to set Bc:
If, periodically, set A is programmed with a member of set Ac and set B is programmed with the congruent member of set Bc, then the two sets, A and B, will remain congruent.
PR-1-6 Invariance Prom Congruence Under Reprogramming (Fig. 1-8)
Given two congruent sets, A and B:
If, periodically, set A is reprogrammed to delete one of its members and set B is reprogrammed to delete the member which is congruent to that member which was deleted from set A, then the two sets, A and B, will remain congruent.
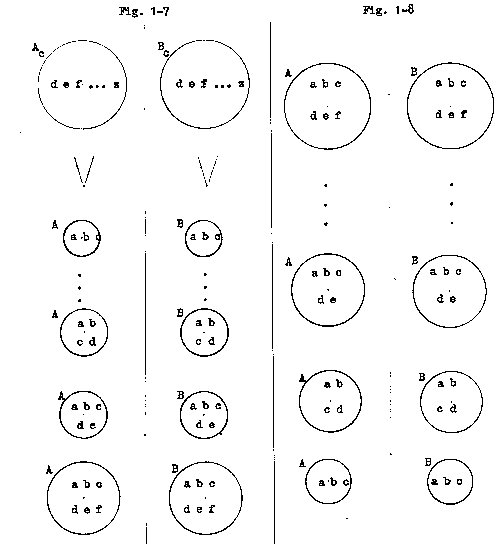
PR-1 -7 Convergence Under Programming (Fig. 1-9)
Given four sets, A, Ac, B and Bc, such that set
A is not congruent to set B and set Ac is congruent to set Bc:
If, periodically, set A is programmed with a member of set Ac and set B is programmed with the congruent member of set Bc, then the two sets, A and B, will converge, approaching congruence as a limit.
PR-1-8 Convergence under Reprogramming (Fig. 1-10)
Given two intersecting sets, A and B:
If, periodically, the subset of set A, B'A, is reprogrammed to delete one of its members and the subset of set B, A'B, is reprogrammed to delete one of its members, then the two sets, A and B, will converge, eventually becoming congruent.
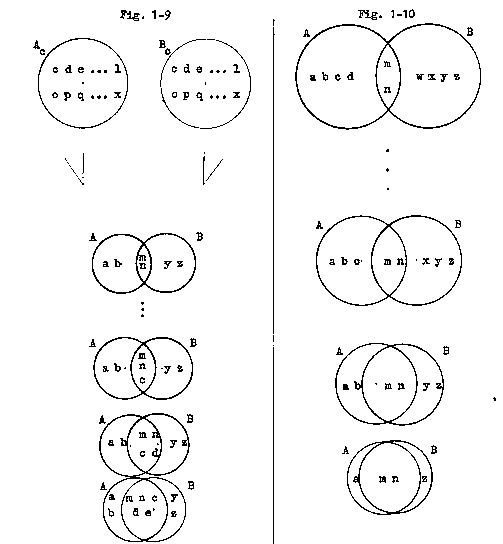
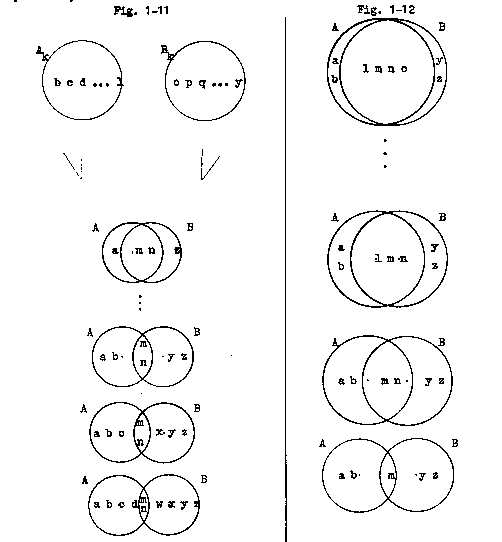
PR-1-9 Divergence Under Programming (Fig. 1-11)
Given four sets, A, Ak, B and Bk, such that set A is not complementary to set B and set Ak is complementary to set Bk:
If, periodically, set A is programmed with a member of Ak and set B is programmed with a member of Bk, then the two sets, A and B, will diverge, approaching a complementary state as a limit.
PR-1-10 Divergence Under Reprogramming (Fig. 1-12)
Given two intersecting sets, A and B:
If, periodically, the common subset of the two sets, A and B, set A(intersect)B, is reprogrammed to delete one of its members, then the two sets, A and B, will diverge, eventually becoming complementary.
The set of properties 1-1 though 1-10 are referred to collectively
as the SET THEORY PROPERTIES. Because of their importance in the text,
we restate them here in a more general form.
PR-1 -1 Integration Through Programming
If two non-congruent sets are programmed with their relative complements, then they will become congruent.
PR-1 -2 Integration Through Reprogramming
If two non-congruent sets are reprogrammed to delete their relative complements, then they will become congruent.
PR-1 -3 Invariance From Complementary State Under Programming
Two complementary sets will remain complementary under programming PROVIDED that no member with which one set is programmed is a member of the other set.
PR-1-4 Invariance From Complementary State Under Reprogramming
Two complementary sets will remain complementary under reprogramming.
PR-1-5 Invariance From Congruence Under Programming
If two congruent sets are programmed with congruent members, then they will remain congruent.
PR-1-6 Invariance From Congruence Under Reprogramming
If two congruent sets are reprogrammed to delete congruent members, then they will remain congruent.
PR-1-7 Convergence Under Programming
If two non-congruent sets are programmed with congruent members, then they tend to converge, approaching congruence as a limit.
PR-1-8 Convergence Under Reprogramming
If two non-congruent sets are reprogrammed to delete members not contained in their intersection, then they converge and eventually become congruent.
PR-1 -9 Divergence Under Programming
If two non-complementary sets are programmed with non-congruent members, then they tend to diverge, approaching a complementary state as a limit.
PR-1 -10 Divergence Under Reprogramming
If two intersecting sets are reprogrammed to delete members contained
in their intersection, then they diverge and eventually become complementary.
THE GENERAL FUNCTION CONCEPT
Let us consider the case of two sets, A and B. We wish to determine
a method for establishing a correspondence between the members of set A
and the members of set B. To accomplish this, we introduce a third set,
C,
and assign to set C the task of performing a certain operation upon
the members of set A which will transform each member of set A into a member
of set B. We then pair each member of set A with that member of set B into
which it was transformed, thus establishing the desired correspondence.
Let us agree to refer to set C as a PROCESSOR since its task is to "process"
the members of set A. For purposes of identification, let us also agree
to refer to set A as the DOMAIN of the processor and set B as the RANGE
of the processor. The members of the domain and range of a processor will
usually be referred to respectively as DOMAIN MEMBERS and RANGE MEMBERS.
The set formed by a specific processor together with its range and domain
is called a FUNCTION.
We refer to that correspondence established between a member of the
domain of a processor and a member of the range of that processor by pairing
the domain member upon which the processor performs a certain operation
with the range member which results from that operation as an ORDERED PAIR.
When it is desired to list ordered pairs, they are presented in the general
form (Domain Member , Range Member), the domain member always being placed
first. The method in which a given function's processor forms ordered pairs
is called the PLAN OF OPERATION of the function.
In a way, one might say that domain members "initiate" the action of
a processor since it is these members upon which the processor performs
a certain operation. Similarly, one might say that range members "terminate"
the action of a processor since these members are the results, so to speak,
of the process.
SPECIAL TERMS
In general discussions, the exact members of the domain and/or the range of a given processor are irrelevant. In such cases, we specify that the domain and/or the range of the given processor is to be considered to indicate that it may (but not necessarily does) contain any member of the technical universal set.
A set so constructed that each of its members is also a member of one
or more of the three basic parts of a function, i.e., a subset of a function,
is called a PROGRAM.
RELATIVITY
The range member with which a given domain member is paired is entirely
relative to the processor doing the pairing. Different processors have
different plans of operation and form different ordered pairs. Because
of this fact, an ordered pair " itself" has no meaning at all; one must
know the processor which formed it for it to have any significance. Hence,
when ordered pairs are listed, if the processor is not obvious from the
context, some form of notation must be employed which will show
the processor. We shall use two forms of notation in this text,
the statement notation and the standard function notation.
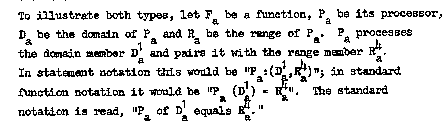
DIAGRAMS
Processors are diagrammed as triangles and their members are specified
(if desired) by placing their names or identifying symbols within the triangle.
Domains and ranges of processors are diagrammed as are average sets.
STATES
In a function, it is the duty of the processor to pair every domain
member with a range member. A given processor may or may not be capable
of doing this. If a processor is capable of assigning a range member to
every domain member it encounters, then the processor is said to be NORMAL.
If, however, there exists any domain member to which the processor is incapable
of assigning a range member, then the processor is said to be ABNORMAL.
If a processor is abnormal, the cause can probably be traced to two
very basic reasons. First, of course, it is possible that the right range
member simply does not exist. However, it is also possible that some subset
of the processor, by its existence, is preventing the processor from choosing
a range member which it would freely pair with the domain member if the
subset were deleted. We refer to such a subset as an INHIBITOR.
It is often desired to change the state of a processor, i.e., force
a normal processor to become abnormal and visa versa. Basically,
the state of a processor can be changed by modifying it and/or its domain.
Many specialized methods can be developed once one becomes familiar with
a specific case.
ABBREVIATIONS
Because certain basic terms in this concept are used frequently throughout
the text, certain standard abbreviations have been chosen. The terms and
their abbreviations are:
| Processor | P or p |
| Domain | D or d |
| Range | R or r |
| Domain member | DM or dm |
| Range member | RM or rm |
| Function | F or f |
| Ordered pair | OP or op |
SUMMARY
The three basic parts of a function - the processor, the domain of the
processor and the range of the processor - are all variables. We may define
the processor so that it will operate any way that we desire it to operate
and we may specify the members of the domain and range at our option. It
should be obvious that virtually everything in existence can be put into
the form of a function by carefully defining these variables - from the
coffee grinder in the corner drug store to the most complex organic structures
In this chapter, we will confine ourselves to general types of functions
and will then expand upon these basic concepts in later chapters.
GENERAL STATIC FUNCTIONS
Since the processor of a function set, it may, like any set, be either
static or dynamic. We refer to a function whose processor is a static set
as a STATIC FUNCTION.
TYPES
Intuition would suggest that a given static function would pair different domain members with different range members, i.e., that the range members chosen would be relative to the domain members processed. It is possible, however, that a processor would pair every domain member with the same range member. We distinguish between these two possibilities by referring to a static function whose processor forms ordered pairs such that the range members of all ordered pairs formed are congruent as a CONSTANT STATIC FUNCTION and referring to a static function whose processor forms ordered pairs such that the range member of each pair is relative to the domain member with which it is paired as a VARIABLE STATIC FUNCTION.
PROPERTIES
Static Function Properties
All static functions conform to the following four properties which
we refer to collectively as the STATIC FUNCTION PROPERTIES. 
Application of Set Theory Properties
Since, as we have said, the processor of a function is a set, we may use any applicable set theory properties in dealing with it. In the case of the static function, we are limited to the two integration properties, integration through programming and integration through reprogramming. However, these two properties are very useful in the light of the first two static function properties. These two properties tell us the characteristics of functions whose processors are congruent and the integration properties tell us how we can make two or more processors congruent.
Special Properties
Often, we are confronted with a situation in which we know some, but not all, of the three basic parts of a given function. Under certain conditions, the unknown parts can be determined; these conditions are given in the following properties

Besides the two possibilities covered by PR-1-15 and PR-1 -16, it is also possible that one would know the ordered pairs that a processor had formed but not the processor. We refer to the act of determining a processor which will form a given set of ordered pairs as RATIONALIZATION.
PR-1 -17 The Rationalization Property
Let Fs be a static function, Ps be its processor, Ds be the
domain of Ps and Rs be the range of Ps.
When every member of
Ds
has been processed by Ps, Ps will have formed
x
ordered pairs.
If n of the x ordered pairs formed by Ps of Fs
are known,
then the configuration of Ps can be approximated, the approximated
configuration approaching the actual configuration as n approaches x.
RELATIONS BETWEEN PROCESSORS
Congruence and Complementary State
In purely theoretical matters, it is convenient to use the standard set theory definitions of congruence and complementary state; however, in applied discussions, such as we will encounter later in the text, it is rather difficult to simply "look" at a processor and see if every member of it is a member of another processor and vice versa.
Consequently, when the set theory definitions become impractical, some other form of definitions must be derived to replace them. When this occurs, we shall use a form centered around the ordered pairs which the processors in question form. From static function I and static function III we know that if two processors process the same domain member, they will pair it with congruent range members if they are congruent and non-congruent range members if they are complementary. We can say, therefore, that two processors are congruent if the sets of ordered pairs which they form from the same domain members are congruent and that two processors are complementary if the sets of ordered pairs which they form from congruent domain members are complementary.
Intersection
When a processor forms an ordered pair, not necessarily all of the processor's members were responsible for the formation. That subset of a processor which is actually responsible for the formation of a given set of ordered pairs is said to be the RELATIVE SUBSET of the processor with respect to the given set of ordered pairs. If two processors intersect, the ordered pairs formed from a given domain member will be congruent if the relative subset is contained in the intersection and non-congruent if it is not. When dealing with functions, then, intersection is simply a combination of congruence and complementary state. Consequently, if two processors intersect, it is convenient to just "split them up" into sufficiently small relative subsets and label the subsets "congruent" or "complementary".
The concept, of which this "idea" is a part, is commonly called COMPARTMENTALIZATION.
SUMMARY
Because of the importance of the properties presented in this article, we restate them here in a more general form.
PR-1-11 Static Function I
Congruent processors will pair congruent domain members with congruent range members.
PR-1-12 Static Function II
Congruent processors will form ordered pairs with non-congruent range members when the domain members processed are not congruent.
PR-1-13 Static Function III
Complementary processors will pair congruent domain members with non-congruent range members.
PR-1-14 Static Function IV
Complementary processors will form ordered pairs with congruent range members only if the domain members processed are not congruent.
PR-1-15 The Prediction Property
The nature of a function's range may be determined through knowledge of its processor and domain.
PR-1-16 The Historical Property
The nature of a function's domain may be determined through knowledge of its processor and range.
PR-1-17 The Rationalization Property
The nature of a function's processor may be determined through knowledge
of the ordered pairs it has formed, the accuracy being relative to the
quantity of ordered pairs known.
GENERAL DYNAMIC FUNCTIONS
A DYNAMIC FUNCTION is a function whose processor is a dynamic set. Since the processor is dynamic, it is continually undergoing modification. The changes which occur in the processor may or may not have some relation to the domain members which are processed. On the basis of the relationship which exists, we subdivide dynamic functions into three basic types as follow:
An INDEPENDENT DYNAMIC FUNCTION is a dynamic function such that the changes which occur in the processor have no relation to the domain members which have been processed.
A TRANSITIONARY DYNAMIC FUNCTION is a dynamic function such that the changes which occur in the processor are partially relative to the domain members which have been processed
A DEPENDENT DYNAMIC FUNCTION is a dynamic function such that the changes which occur in the processor are relative to and only to the domain members which have been processed.
We have little use in this text for the independent dynamic function and the transitionary dynamic function and we shall not discuss them further. We devote the remainder of this article to the properties of the dependent dynamic function.
DEPENDENT DYNAMIC FUNCTIONS
Dependent Dynamic vs. Static
Let us consider the case of a static processor, Ps. Ps encounters the domain member D1 and pairs it with the range member R1. The process then ends. If Ps would again encounter D1, then it would again pair it with R1 - over and over again.
Now, let us consider the case of a dependent dynamic processor, Pd. Pd encounters the domain member D1 and pairs it with the range
member R1. Then something "happens" to Pd. By
definition, it undergoes some change which is relative to and only to D1.
D1 has "left its mark", so to speak, upon Pd. If
Pd would again encounter D1, it would not necessarily
pair it with R1. It could, of course, but it need not - for
Pd has changed; compared to the Pd a few moments
ago (before D1 was processed) it is a different processor.
Special Relativity
As the processor of a dependent dynamic function forms an ordered pair, certain members come into being whose characteristics are relative to the domain member being processed. When the ordered pair has been formed, these members become part of the processor and contribute to the formation of all future ordered pairs. As the processor forms more and more ordered pairs, it receives more and more such members. We refer to these members which have been added to the processor of a dependent dynamic function because of domain members which have been processed as the processor's PROGRAMMING.
In any function, the range members which are paired with a given set of domain members (hence, the ordered pairs which are formed), are relative to and only to that function's processor. But, in a dependent dynamic function, the processor changes every time it forms an ordered pair because it receives new programming relative to the domain member it just processed. Because of this, the processor of a dependent dynamic function is actually relative to the domain members it has processed (hence, the ordered pairs it has formed).
Since ordered pairs are relative to the processor (in any function) and the processor is relative to all previous ordered pairs formed (in a dependent dynamic function), one may conclude that, in a dependent dynamic function, a given ordered pair is actually relative to all ordered pairs which were formed before it.

We refer to a sequence of events, each succeeding phase of which is determined by all preceding phases as a CONTINUUM. A subset of a continuum, i.e., some part of the sequence, is called an INTERIM. We say that the ordered pairs formed by the processor of a dependent dynamic function form a continuum when placed in Gamma sequence.
Notation
Because of the significance of the sequence in which ordered pairs are
formed in a dependent dynamic function, the conventional notations we discussed
earlier are usually of little value. We therefore expand the standard function
notation so that the additional variables are taken into consideration.
We shall present ordered pairs formed by dependent dynamic functions in
the general form

The specification of a definite interim allows us to omit any preceding or succeeding operations in which we may not be interested. The specific applications of this notation, the form may be abbreviated to exclude any unnecessary material; however, as this is done, one approaches the original standard function notation.
Application of Static Function Properties
As we have stated, a dependent dynamic function's processor undergoes
programming upon completion of the formation of each ordered pair. During
the interim between the time it completes the formation of an ordered pair
and the time it begins to process another domain member, however, it undergoes
no modification. We refer to this interim as an INSTANT. During each instant,
the processor is static and, consequently, all static function properties
are applicable.
Application of Set Theory Properties
Since we are dealing with dynamic sets, all ten set theory properties apply. Of special interest, however, are the four properties which deal with dynamic sets undergoing programming, for, as we have said, a dependent dynamic function's processor undergoes programming each time it forms an ordered pair. To see the possible applications more clearly, we restate these properties here, applied to our discussion.
Invariance From Complementary State Under Programming.
If two dependent dynamic functions have complementary processors, then they will probably remain complementary if the processor's domains remain complementary.
Invariance From Congruence Under Programming
If two dependent dynamic functions have congruent processors, then they will remain congruent if the processors process congruent domain members in identical sequences.
Convergence Under Programming
If two dependent dynamic functions have non-congruent processors, then they will converge if the processors continue to process congruent domain members in identical sequences.
Divergence Under Programming
If two dependent dynamic functions have non-complementary processors, then they will tend to diverge if the processor's domains remain complementary.
The second property given is absolute; the others are approximations. In general, the probability is in favor of their occurrence, but they not necessarily true in all cases. However, in applied discussions, all are quite useful.
The Projection Property
The static function properties, which may be applied to dependent dynamic functions during instants, become much more useful when one has a method of "following" the processor as it changes from instant to instant. The Projection Property is designed to fill this gap.
PR-1-18 The Projection Property
Let Fv be a dependent dynamic function and Pv
be its processor. Pvat time = T can be determined if Pv
at time = (T-X) is known and all ordered pairs formed by Pv
during the interim X are known in Gamma sequence.
Change of State
Like any function, a dependent dynamic function may be normal or abnormal. However, when one discusses methods of changing the state, a few more factors become relative. In all functions, state may be changed by modification of the processor and/or its domain. In this case, however, the processor is continually undergoing modification, this modification being relative to the domain members processed. Consequently, one might be able to change state simply by changing the sequence in which the domain members are processed.
Again, more sophisticated methods are best developed when one is dealing
with a special case, but the fact that a processor is dynamic adds many
additional possibilities.
POWER AND CONTROL
POWER

Interpretation
We are given a certain dependent dynamic function and we wish that function's processor to choose from its range a certain range member and pair it with some domain member. It is not relevant which domain member is used; it is relevant only that a certain previously selected range member is paired with a domain member. The General Power Axiom tells us that whatever range member we choose, we can find a domain member with which that function's processor will pair it.
When the General Power Axiom is applied to a special case, there are two basic possibilities.
First, it is possible that, for the range member we have chosen, there is a domain member which, if processed now, would be paired with it. If this is the case, then Z need only consist of one member.
Secondly, however, it is also possible that, at present, no domain member
exists which the processor will pair with our chosen range member. In this
case, it is necessary to modify the processor so that a domain member does
exist. We recall that, in dependent dynamic functions, the processor is
continually changing and that this change is relative to the domain members
processed. To modify the processor, then, we define a subset of the processor's
domain, Z, such that its members, when processed in a certain sequence,
will change the processor in such a manner that the last domain member
of the sequence will be paired with our chosen range member.
CONTROL
When a function's processor encounters a domain member, it "takes" the member and performs a certain operation upon it. At the conclusion of this process, the domain member has been transformed into a range member. Range members, then, are the results of the operations of a processor - the things they "produce", so to speak. We wish to determine a basic method by which the range members yielded by a processor can be controlled.
The General Power Axiom tells us that, in a dependent dynamic function, for any range member we choose, there exists a domain member which, if processed, would be paired with the chosen range member. The axiom tells us that this resource exists, but not how to tap it. Obviously, if we knew the "right" domain members to use, we could control the function.
The range member which is formed from a given domain member is relative to the processor. Hence, if we are familiar with the method in which a given processor forms ordered pairs, we can figure out what domain member need be processed to yield a certain range member. If our examination reveals that no domain member exists which will do this, we can change the processor (of a dependent dynamic function) so that a domain member does exist by allowing it to process certain carefully selected domain members. Once the processor has been sufficiently modified, we can obtain our desired range member.
The fact that the processor of a dependent dynamic function changes each time it processes a domain member provides a convenient method of modifying it. However, the sane results could be obtained by simply "taking" the processor and directly modifying it so that it conforms to our wishes. In this case, since the changes would not now be completely relative to the domain members processed, the function would become a transitionary dynamic function.
Similarly, one could apply the General Power Axiom to static functions by arbitrarily modifying their processors so that desired range members could be obtained. During the period of modification, the static functions would become independent dynamic functions, their change being relative to the person or thing doing the modifying (as opposed to the domain members processed).
In all of these cases, control of the range members produced has depended upon an intimate knowledge of the inner workings of the processor of the function involved - the processor's plan of operation. Once this is known, many elaborate methods of control can be derived.
So far, we have discussed functions - static and dynamic. But, when
we use the term "function" in its most general sense, what do we mean?
As we have said, virtually everything can be put into the form of a function.
Consequently, virtually anything can be controlled if one is intimately
familiar with the method in which it operates.
We formally state these conclusions in the General Control Theorem.
T-1 -1 General Control TheoremAnything can be controlled through knowledge of its plan of operation.